-
Exercice N° 1
Un alternateur triphasé étoile à une tension (entre phases) U = 660 V et débite un courant de 500 A sous un cos j = 0,8 (inductif) à la fréquence f = 50 Hz.
1) Calculer la puissance apparente, la puissance active et la puissance réactive.
2) Sachant que l’induit comporte 372 conducteurs et que le flux sous un pôle est de 0,0027 Wb. Calculer le coefficient de Kapp en admettant que E est égal à la tension sur une phase à la sortie de l’alternateur.
Toucher pour afficher la solution
1) Puissance apparente, active et réactive
Puissance active
P=√ 3U.I,cosf = 457,26 K W
Puissance réactive
Q=√ 3U.I,sinf = 342,95 K VAR
Puissance apparente
S=√ 3U.I = 571,58 K W
2) Coefficient de Kapp
Pour un alternateur triphasé, la fem par phase s’exprime par la relation: E = Knffm
Où K est le coefficient de Kapp
n = 372 / 3 = 124 le nombre de conducteurs par phase
f = 50Hz la fréquence
fm = 0,0027Wb le flux sous un pôle.
En confondant la tension de sortie et la fem, c’est à dire en négligeant les chutes de tension dans l’alternateur, E = 381V et K= 22,7 SI
-
Exercice N° 2
Un alternateur monophasé fournit un courant de 50 A sous une tension de 240 V et avec un facteur de puissance de 0,8 (charge inductive). Le rotor consomme 8 A sous une tension de 35 V, les pertes constantes sont de 450 W et la résistance de l’enroulement du stator est R=0,2 W.
1) Calculer la puissance utile de l’alternateur et son rendement.
2) Pour la même excitation on a relevé: Ev = 280 V et Icc= 40 A. Calculer l’impédance et la réactance interne de l’alternateur et déterminer la f.e.m. (Ev) par le graphique de Behn-Eschenburg.
Toucher pour afficher la solution
Correction
1) Puissance utile et rendement
La puissance utile est donnée par la relation:
Pu = UI cos f = 9,6 kW
La puissance absorbée étant donnée par:
Pabs = Pu + Pjs + Pjr + Pc = 10,83 kW
Avec
Pjr = ui = 280W
Pjs = RI2 = 500W
Pc = 450W
Le rendement est
h = Pu / Pabs = 0,89
2) Impédance et réactance internes, fém.
L’impédance interne est obtenue à partir de la mesure de la fem et du courant de court-circuit. Elle est peu différente de la réactance interne.
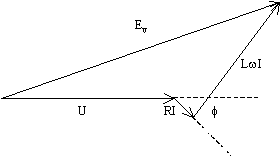
Pour obtenir la fem on trace le diagramme de Behn-Eschenburg
En projetant sur un axe horizontal Ox et un axe vertical Oy, on obtient
Evx = U + RI cosf + LwI sin f = 458 V
Evy = – RI sin f + LwI cos f = 274 V
Ev2 = Evx2 + Evx2 Ev = 534 Vbit de 400 A sous 420 V de tension composée.
-
Exercice N° 3
Un alternateur triphasé étoile fournit un courant de 400 A sous une tension composée de 420 V et avec un facteur de puissance de 0,9 (charge inductive). La résistance mesurée entre phases du stator est R = 0,03 W et l’ensemble des pertes constantes et par effet Joule au rotor est P = 6 kW.
1) Calculer la puissance utile de l’alternateur et son rendement
2) Pour la même excitation on a relevé : Eve = 510 V (entre phases) et Icc = 300 A. Calculer la réactance interne (R est ici négligée) et déterminer la f.é.m. (Eve) entre phases qui correspond à un débit de 400 A sous 420 V de tension composée.
Toucher pour afficher la solution
Correction
1) Puissance utile et rendement
La puissance utile est donnée par
Pu=√ 3.U.I,cosf = 261,89 K W
La puissance absorbée étant quant à elle
Pabs = Pu + Pjs + Pjr + Pfs + Pm = Pu + Pjs + Pjr + Pc
Pjs = ( 3/2 )RI2 = 7938 W représente les pertes Joule au stator
Pjr, les pertes Joule au rotor
Pfs, les pertes fer au stator
Pm les pertes mécaniques
Pc = Pfr + Pm, les pertes constantes
D’où la puissance absorbée
Pabs = 275,82 kW
Et le rendement
h = Pu / Pabs = 0,95
2) Réactance interne et fem
La résistance interne étant négligée on a la réactance interne
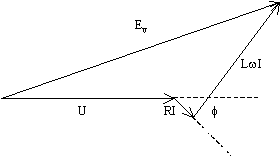
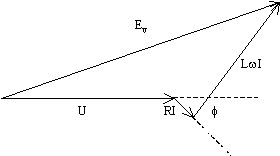
On détermine alors la fem sur une phase à partir du diagramme de Behn Eschenburg
En projetant sur des axes, horizontal (Ox) et Vertical (Oy)
Evx = V + RI cos f + LwI sin f =
Evy = – RI sin f + LwI cos f =
La fem entre phases est alors
-
Exercice N° 4
